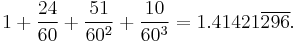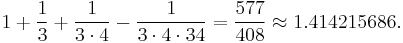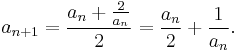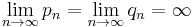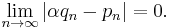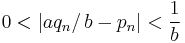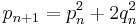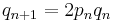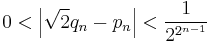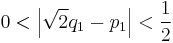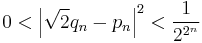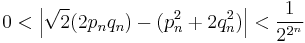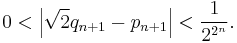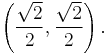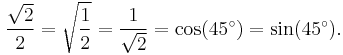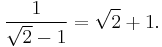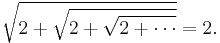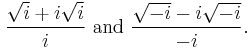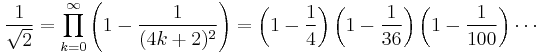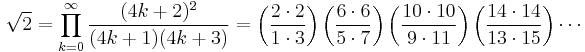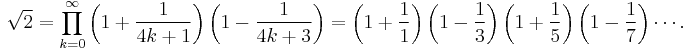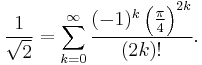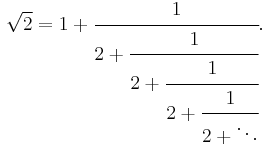Square root of 2

The square root of 2 is equal to the length of the hypotenuse of a right triangle with legs of length 1.

The square root of 2, often known as root 2, is the positive real number that, when multiplied by itself, gives the number 2.

Geometrically the square root of 2 is the length of a diagonal across a square with sides of one unit of length; this follows from the Pythagorean theorem. It was probably the first number known to be irrational. Its numerical value truncated to 65 decimal places^[1] is:

1.41421 35623 73095 04880 16887 24209 69807 85696 71875 37694 80731 76679 73799....

The square root of 2.

The quick approximation 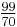$\tfrac{99}{70}$ for the square root of two is most frequently used. Despite having a denominator of only 70, it differs from the correct value by less than 1/10,000.

List of numbers – Irrational and suspected irrational numbers γ – ζ(3) – √2 – √3 – √5 – φ – ρ – δ_S – α – e – π – δ
Binary	1.0110101000001001111...
Decimal	1.4142135623730950488...
Hexadecimal	1.6A09E667F3BCC908B2F...
Continued fraction	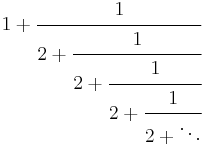$1 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \ddots}}}}$

1 History
2 Computation algorithms
3 Proofs of irrationality
4 Properties of the square root of two
5 Series and product representations
6 Continued fraction representation
7 Paper size
8 See also
9 Notes
10 References
11 External links

History

Babylonian clay tablet YBC 7289 with annotations.

The Babylonian clay tablet YBC 7289 (c. 1800–1600 BCE) gives an approximation of $\sqrt{2}$ in four sexagesimal figures, which is about six decimal figures:^[2]

$1 + \frac{24}{60} + \frac{51}{60^2} + \frac{10}{60^3} = 1.41421\overline{296}.$

Another early close approximation of this number is given in ancient Indian mathematical texts, the Sulbasutras (c. 800–200 BCE) as follows: Increase the length [of the side] by its third and this third by its own fourth less the thirty-fourth part of that fourth.^[3] That is,

$1 + \frac{1}{3} + \frac{1}{3 \cdot 4} - \frac{1}{3 \cdot4 \cdot 34} = \frac{577}{408} \approx 1.414215686.$

This ancient Indian approximation is the seventh in a sequence of increasingly accurate approximations based on the sequence of Pell numbers, that can be derived from the continued fraction expansion of $\sqrt{2}.$

Pythagoreans discovered that the diagonal of a square is incommensurable with its side, or in modern language, that the square root of two is irrational. Little is known with certainty about the time or circumstances of this discovery, but the name of Hippasus of Metapontum is often mentioned. For a while, ancient Greeks treated as an official secret the discovery that the square root of two is irrational, and, according to legend, Hippasus was murdered for divulging it.^[4]^[5]^[6]

Computation algorithms

There are a number of algorithms for approximating the square root of 2, which in expressions as a ratio of integers or as a decimal can only be approximated. The most common algorithm for this, one used as a basis in many computers and calculators, is the Babylonian method^[7] of computing square roots, which is one of many methods of computing square roots. It goes as follows:

First, pick a guess, a₀ > 0; the value of the guess affects only how many iterations are required to reach an approximation of a certain accuracy. Then, using that guess, iterate through the following recursive computation:

$a_{n+1} = \frac{a_n + \frac{2}{a_n}}{2}=\frac{a_n}{2}+\frac{1}{a_n}.$

The more iterations through the algorithm (that is, the more computations performed and the greater "n"), the better approximation of the square root of 2 is achieved. Each iteration approximately doubles the number of correct digits. Starting with a₀ = 1 the next approximations are

3/2 = 1.5
17/12 = 1.416...
577/408 = 1.414215...
665857/470832 = 1.4142135623746...

The value of √2 was calculated to 137,438,953,444 decimal places by Yasumasa Kanada's team in 1997.

In February 2006 the record for the calculation of √2 was eclipsed with the use of a home computer. Shigeru Kondo calculated 200,000,000,000 decimal places in slightly over 13 days and 14 hours using a 3.6 GHz PC with 16 GiB of memory.^[8]

Among mathematical constants with computationally challenging decimal expansions, only π has been calculated more precisely.^[9]

Proofs of irrationality

A short proof of this result is to obtain it from rational root theorem, that if p(x) is a monic polynomial with integer coefficients, then any rational root of p(x) is necessarily an integer. Applying this to the polynomial p(x) = x² − 2, it follows that √2 is either an integer or irrational. Since √2 is not an integer (2 is not a perfect square), √2 must therefore be irrational.

See quadratic irrational for a proof that the square root of any non-square natural number is irrational.

It is not known whether √2 is a normal number, a stronger property than irrationality, but statistical analyses of its binary expansion are consistent with the hypothesis that is normal to base two.^[10]

Proof by infinite descent

One proof of the number's irrationality is the following proof by infinite descent. It is also a proof by contradiction, which means the proposition is proved by assuming that the opposite of the proposition is true and showing that this assumption is false, thereby implying that the proposition must be true.

Assume that √2 is a rational number, meaning that there exists an integer a and an integer b in general such that a / b = √2.
Then √2 can be written as an irreducible fraction a / b such that a and b are coprime integers and (a / b)² = 2.
It follows that a² / b² = 2 and a² = 2 b². ( (a / b)ⁿ = aⁿ / bⁿ )
Therefore a² is even because it is equal to 2 b². (2 b² is necessarily even because it is 2 times another whole number; that is what "even" means.)
It follows that a must be even (as squares of odd integers are themselves odd).
Because a is even, there exists an integer k that fulfills: a = 2k.
Substituting 2k from (6) for a in the second equation of (3): 2b² = (2k)² is equivalent to 2b² = 4k² is equivalent to b² = 2k².
Because 2k² is divisible by two and therefore even, and because 2k² = b², it follows that b² is also even which means that b is even.
By (5) and (8) a and b are both even, which contradicts that a / b is irreducible as stated in (2).

Q.E.D.

Since there is a contradiction, the assumption (1) that √2 is a rational number must be false. By the law of excluded middle, the opposite is proven: √2 is irrational.
This proof was given by Euclid.

Proof by unique factorization

An alternative proof uses the same approach with the fundamental theorem of arithmetic which says every integer greater than 1 has a unique factorization into powers of primes.

Assume that √2 is a rational number. Then there are integers a and b such that a is coprime to b and √2 = a / b. In other words, √2 can be written as an irreducible fraction.
The value of b cannot be 1 as there is no integer a the square of which is 2.
There must be a prime p which divides b and which does not divide a otherwise the fraction would not be irreducible.
The square of a can be factorized as the product of the primes into which a is factorized but with each power doubled.
Therefore by unique factorization the prime p which divides b, and also its square, cannot divide the square of a.
Therefore the square of an irreducible fraction cannot be reduced to an integer.
Therefore the square root of 2 cannot be a rational number.

This proof can be generalized to show that any root of any natural number which is not the square of a natural number is irrational. The article quadratic irrational gives a proof of the same result but not using the fundamental theorem of arithmetic.

Proof by infinite descent, not involving factoring

The following reductio ad absurdum argument showing the irrationality of √2 is less well-known. It uses the additional information 2 > √2 > 1 so that 1 > √2 − 1 > 0.^[11]

Assume that √2 is a rational number. This would mean that there exist positive integers m and n with n ≠ 0 such that m/n = √2. Then m = n√2 and m√2 = 2n.
We may assume that n is the smallest integer so that n√2 is an integer. That is, that the fraction m/n is in lowest terms.
Then $\sqrt{2} = \frac{m}{n}=\frac{m(\sqrt{2}-1)}{n(\sqrt{2}-1)}=\frac{2n-m}{m-n}$
Since 1 > √2 − 1 > 0, it follows that n > n(√2 − 1) = m − n > 0.
So the fraction m/n for √2, which according to (2) is already in lowest terms, is represented by (3) in strictly lower terms. This is a contradiction, so the assumption that √2 is rational must be false.

Geometric proof

Another reductio ad absurdum showing that √2 is irrational is less well-known.^[12] It is also an example of proof by infinite descent. It makes use of classic compass and straightedge construction, proving the theorem by a method similar to that employed by ancient Greek geometers. It is essentially the previous proof viewed geometrically.

Let ABC be a right isosceles triangle with hypotenuse length m and legs n. By the Pythagorean theorem, m/n = √2. Suppose m and n are integers. Let m:n be a ratio given in its lowest terms.

Draw the arcs BD and CE with centre A. Join DE. It follows that AB = AD, AC = AE and the ∠BAC and ∠DAE coincide. Therefore the triangles ABC and ADE are congruent by SAS.

Since ∠EBF is a right angle and ∠BEF is half a right angle, BEF is also a right isosceles triangle. Hence BE = m − n implies BF = m − n. By symmetry, DF = m − n, and FDC is also a right isosceles triangle. It also follows that FC = n − (m − n) = 2n − m.

Hence we have an even smaller right isosceles triangle, with hypotenuse length 2n − m and legs m − n. These values are integers even smaller than m and n and in the same ratio, contradicting the hypothesis that m:n is in lowest terms. Therefore m and n cannot be both integers, hence √2 is irrational.

Analytic proof

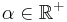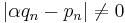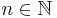Lemma 1: let $\alpha \in \mathbb{R}^+$ and $p_1,p_2,\dots, q_1, q_2, \ldots \in \mathbb{N}$ such that $\left|\alpha q_n - p_n \right| \neq 0$ for all $n \in \mathbb{N}$ and

$\lim_{n \rightarrow \infty} p_n = \lim_{n \rightarrow \infty} q_n = \infty\,$

$\lim_{n \rightarrow \infty} \left| \alpha q_n - p_n \right| = 0.\,$

Then α is irrational.

Proof: suppose α = a/b with a, b ∈ N⁺.

For sufficiently big n,

$0 < \left| \alpha q_n - p_n \right| < \frac{1}{b}$

then

$0 < \left| a q_n /\ \! b - p_n \right| < \frac{1}{b}$

$0 < \left| a q_n - b p_n \right| < 1 \,$

but aq_n − bp_n is an integer, absurd, then α is irrational.

√2 is irrational.

Proof: let p₁ = q₁ = 1 and

$p_{n+1} = p_n^2 + 2 q_n^2 \,$

$q_{n+1} = 2 p_n q_n \,\!$

for all n ∈ N.

By induction,

$0 < \left| \sqrt{2} q_n - p_n \right| < \frac{1}{2^{2^{n-1}}}$

for all n ∈ N. For n = 1,

$0 < \left| \sqrt{2} q_1 - p_1 \right| < \frac{1}{2}$

and if is true for n then is true for n + 1. In fact

$0 < \left| \sqrt{2} q_n - p_n \right|^2 < \frac{1}{2^{2^n}}$

$0 < \left| \sqrt{2} (2 p_n q_n) - (p_n^2 + 2 q_n^2) \right| < \frac{1}{2^{2^n}}$

$0 < \left| \sqrt{2} q_{n + 1} - p_{n + 1} \right| < \frac{1}{2^{2^n}}.$

By lemma 1 applications √2 is irrational.

Constructive proof

Given integers a and b, since the valuation of 2b² is odd, while the valuation of a² is even, they must be distinct integers, so that 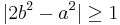$|2 b^2 - a^2| \geq 1$ . An easy calculation then yields a lower bound of 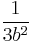$\frac{1}{3b^2}$ for the difference 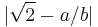$|\sqrt2 - a / b|$ , yielding a direct proof of irrationality not relying on the law of excluded middle, see Errett Bishop (1985, p. 18).

Properties of the square root of two

One-half of √2, approximately 0.70710 67811 86548, is a common quantity in geometry and trigonometry because the unit vector that makes a 45° angle with the axes in a plane has the coordinates

$\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right).$

This number satisfies

$\frac{\sqrt{2}}{2} = \sqrt{\frac{1}{2}} = \frac{1}{\sqrt{2}} = \cos(45^\circ) = \sin(45^\circ).$

One interesting property of the square root of two is as follows:

$\!\ {1 \over {\sqrt{2} - 1}} = \sqrt{2} + 1.$

This is a result of a property of silver means.

Another interesting property of the square root of two:

$\sqrt{2+\sqrt{2+\sqrt{2 + \cdots}}} = 2. \,$

The square root of two can also be expressed in terms of the copies of the imaginary unit i using only the square root and arithmetic operations:

$\frac{\sqrt{i}+i \sqrt{i}}{i}\text{ and }\frac{\sqrt{-i}-i \sqrt{-i}}{-i}.$

The square root of two is also the only real number other than 1 whose infinite tetrate is equal to its square.

$\sqrt{2}^ {\sqrt{2}^ {\sqrt{2}^ {\ \cdot^ {\cdot^ \cdot}}}} = 2$

The square root of two can also be used to approximate π:

$2^m\sqrt{2-\sqrt{2+\sqrt{2+\cdots+\sqrt{2}}}} \to \pi\text{ as }m \to \infty\,$

for m square roots and only one minus sign.^[13]

Series and product representations

The identity cos(π/4) = sin(π/4) = 1/√2, along with the infinite product representations for the sine and cosine, leads to products such as

$\frac{1}{\sqrt 2} = \prod_{k=0}^\infty \left(1-\frac{1}{(4k+2)^2}\right) = \left(1-\frac{1}{4}\right) \left(1-\frac{1}{36}\right) \left(1-\frac{1}{100}\right) \cdots$

and

$\sqrt{2} = \prod_{k=0}^\infty \frac{(4k+2)^2}{(4k+1)(4k+3)} = \left(\frac{2 \cdot 2}{1 \cdot 3}\right) \left(\frac{6 \cdot 6}{5 \cdot 7}\right) \left(\frac{10 \cdot 10}{9 \cdot 11}\right) \left(\frac{14 \cdot 14}{13 \cdot 15}\right) \cdots$

or equivalently,

$\sqrt{2} = \prod_{k=0}^\infty \left(1+\frac{1}{4k+1}\right) \left(1-\frac{1}{4k+3}\right) = \left(1+\frac{1}{1}\right) \left(1-\frac{1}{3}\right) \left(1+\frac{1}{5}\right) \left(1-\frac{1}{7}\right) \cdots.$

The number can also be expressed by taking the Taylor series of a trigonometric function. For example, the series for cos(π/4) gives

$\frac{1}{\sqrt{2}} = \sum_{k=0}^\infty \frac{(-1)^k \left(\frac{\pi}{4}\right)^{2k}}{(2k)!}.$

The Taylor series of √(1 + x) with x = 1 and using the double factorial n!! gives

$\sqrt{2} = \sum_{k=0}^\infty (-1)^{k+1} \frac{(2k-3)!!}{(2k)!!} = 1 + \frac{1}{2} - \frac{1}{2\cdot4} + \frac{1\cdot3}{2\cdot4\cdot6} - \frac{1\cdot3\cdot5}{2\cdot4\cdot6\cdot8} + \cdots.$

The convergence of this series can be accelerated with an Euler transform, producing

$\sqrt{2} = \sum_{k=0}^\infty \frac{(2k+1)!}{(k!)^2 2^{3k+1}} = \frac{1}{2} +\frac{3}{8} + \frac{15}{64} + \frac{35}{256} + \frac{315}{4096} + \frac{693}{16384} + \cdots.$

It is not known whether √2 can be represented with a BBP-type formula. BBP-type formulas are known for π√2 and √2 ln(1 + √2), however. [1]

Continued fraction representation

The square root of two has the following continued fraction representation:

$\!\ \sqrt{2} = 1 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \ddots}}}}.$

The convergents formed by truncating this representation form a sequence of fractions that approximate the square root of two to increasing accuracy, and that are described by the Pell numbers (known as side and diameter numbers to the ancient Greeks due to their use in approximating the ratio between the sides and diagonal of a square). The first convergents are: 1/1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, 577/408. The convergent p/q differs from the square root of 2 by almost exactly 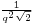$\scriptstyle{\frac{1}{q^2\sqrt{2}}}$ and then the next convergent is (p + 2q)/(p + q).

Paper size

The square root of two is the aspect ratio of paper sizes under ISO 216 (A4, A0, etc.). This ratio guarantees that cutting in half a sheet by a line parallel to its short side results in two sheets having the same ratio.

Notes

↑ (sequence A002193 in OEIS)
↑ Fowler and Robson, p. 368.
Photograph, illustration, and description of the root(2) tablet from the Yale Babylonian Collection
High resolution photographs, descriptions, and analysis of the root(2) tablet (YBC 7289) from the Yale Babylonian Collection
↑ Henderson.
↑ Stephanie J. Morris, "The Pythagorean Theorem", Dept. of Math. Ed., University of Georgia.
↑ Brian Clegg, "The Dangerous Ratio ...", Nrich.org, November 2004.
↑ Kurt von Fritz, "The discovery of incommensurability by Hippasus of Metapontum", Annals of Mathematics, 1945.
↑ Although the term "Babylonian method" is common in modern usage, there is no direct evidence showing how the Babylonians computed the approximation of √2 seen on tablet YBC 7289. Fowler and Robson offer informed and detailed conjectures.
Fowler and Robson, p. 376. Flannery, p. 32, 158.
↑ http://numbers.computation.free.fr/Constants/Miscellaneous/Records.html Constants and Records of Computation
↑ Number of known digits
↑ Good & Gover (1967).
↑ Gardner, Martin (2001), A Gardner's workout: training the mind and entertaining the spirit, A K Peters, Ltd., ISBN 9781568811208 , p. 16
↑ Apostol (2000), p. 841
↑ What is mathematics?, Richard Courant, Herbert Robbins, p. 124

References

Apostol, Tom M. (2000), "Irrationality of the square root of two – A geometric proof", American Mathematical Monthly 107 (9): 841–842, doi:10.2307/2695741, http://jstor.org/stable/2695741 .
Bishop, Errett (1985), Schizophrenia in contemporary mathematics. Errett Bishop: reflections on him and his research (San Diego, Calif., 1983), 1--32, Contemp. Math. 39, Amer. Math. Soc., Providence, RI.
Flannery, David (2005), The Square Root of Two, Springer-Verlag, ISBN 0-387-20220-X .
Fowler, David; Robson, Eleanor (1998), "Square Root Approximations in Old Babylonian Mathematics: YBC 7289 in Context", Historia Mathematica 25 (4): 366–378, doi:10.1006/hmat.1998.2209, http://www.hps.cam.ac.uk/dept/robson-fowler-square.pdf .
Good, I. J.; Gover, T. N. (1967), "The generalized serial test and the binary expansion of √2", Journal of the Royal Statistical Society, Series A 130 (1): 102–107, doi:10.2307/2344040, http://www.jstor.org/stable/2344040 .
Henderson, David W. (2000), "Square roots in the Śulba Sūtras", in Gorini, Catherine A., Geometry At Work: Papers in Applied Geometry, Cambridge University Press, pp. 39–45, ISBN 9780883851647, http://www.math.cornell.edu/~dwh/papers/sulba/sulba.html .

External links

Gourdon, X.; Sebah, P. (2001), "Pythagoras' Constant: √2", Numbers, Constants and Computation, http://numbers.computation.free.fr/Constants/Sqrt2/sqrt2.html .
Weisstein, Eric W., "Pythagoras's Constant" from MathWorld.
The Square Root of Two to 5 million digits by Jerry Bonnell and Robert Nemiroff. May, 1994.
Square root of 2 is irrational, a collection of proofs
√2.net, enthusiast site with realtime computation